Physics Constrained Learning

Overview

In the rapidly evolving field of machine learning, establishing a robust workflow is crucial. A typical workflow encompasses several stages: identifying a problem, curating data, designing an architecture, crafting a loss function, and employing optimization techniques. By integrating physics-based priors into each stage, we can develop models that are not only robust and capable of learning from small sample sizes but are also truly reflective of underlying physical principles rather than merely fitting curves. This approach paves the way for creating models that can generalize well and potentially simulate real-world physics accurately.

Physics constrained loss function

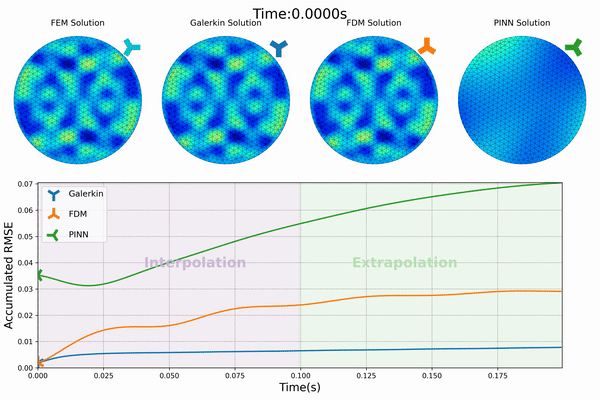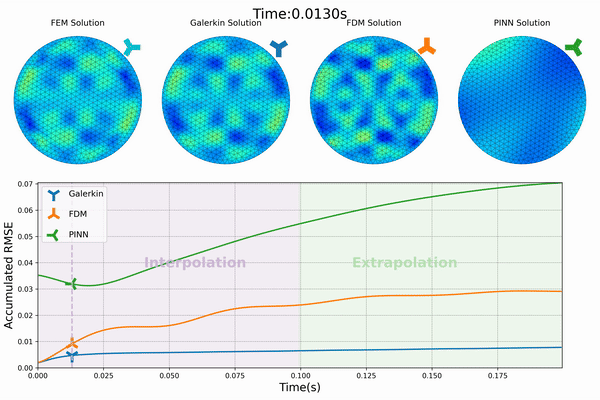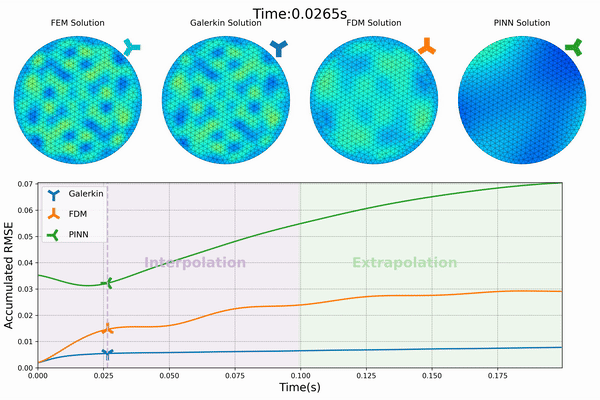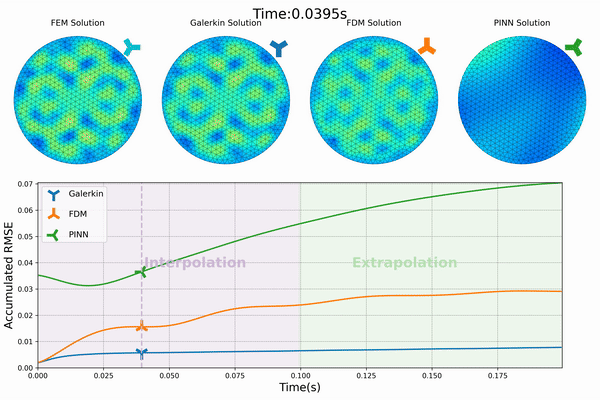
Our project’s first phase has successfully integrated physics priors into the machine learning workflow, particularly within the loss function design. We have developed “Physics-Constrained Graph Galerkin Learning,” an innovative method tailored for solving spatio-temporal partial differential equations (PDEs). This method combines the Galerkin method for spatial discretization with an autoregressive scheme for capturing temporal dynamics. Conceptualized through a map-reduce operation, the mapping phase of our approach is fully parallelizable, and the reduction phase leverages Sparse Matrix Multiplication (SPMM). This integration is operationalized within a graph-based network framework, utilizing native PyTorch operators for seamless execution across diverse computing platforms. (Wen et al., 2024)

Comparison of long-term rollout between Galerkin loss autoregressive model and data loss one.

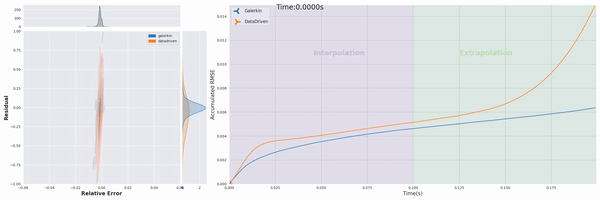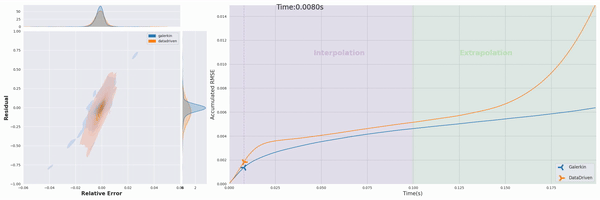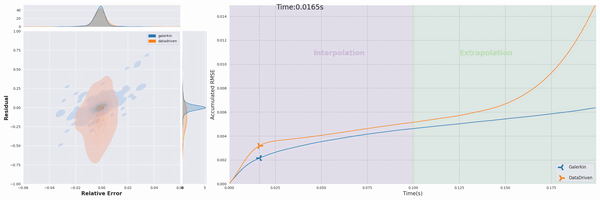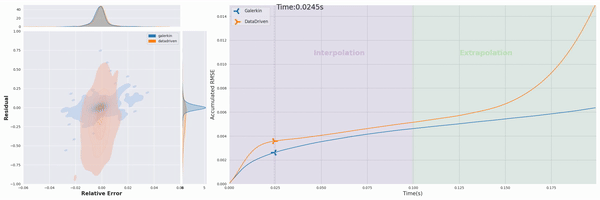
The efficiency of our approach is further enhanced by minimizing the computational graph, which facilitates rapid back-propagation and enhances overall performance. Our method has shown to achieve training speeds comparable to those of data-driven loss models and excels in scalability, efficiency, accuracy, and capability for long-term predictions.

Comparison of learning efficiency and convergent speed between Galerkin loss model and data loss model.

We introduce the physics-constrained graph Galerkin learning, an approach for solving spatio-temporal partial differential equations (PDEs) that leverages Galerkin discretized variational loss within a graph-based network framework. This method integrates the Galerkin method for spatial discretization with an autoregressive scheme for temporal dynamics. We conceptualize the Galerkin process as a map-reduce operation, where the mapping phase is entirely parallelizable and the reduction phase employs Sparse Matrix Multiplication (SPMM). Leveraging native PyTorch operators ensures seamless and efficient execution across a variety of devices and platforms, while minimizing the computational graph to facilitate rapid back-propagation and boost overall performance. Our method not only achieves training speeds comparable to those of data-driven loss models but also excels in scalability, efficiency, accuracy, and long-term rollouts. Experiments on canonical PDEs, including parabolic and hyperbolic types, demonstrate that our method outperforms previous physical based learning paradigms, such as physics-informed loss and finite-difference-induced loss, as well as data-driven method.

Overview

Physics constrained loss function

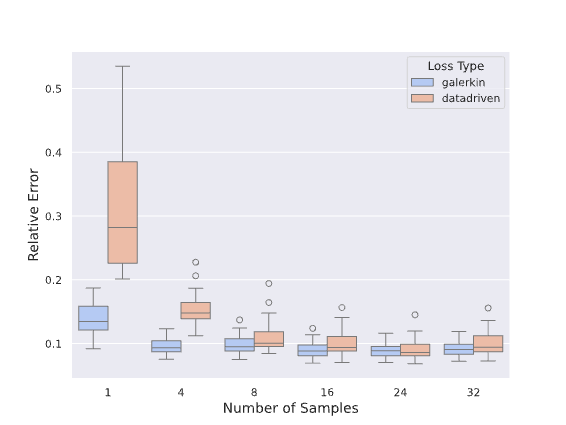
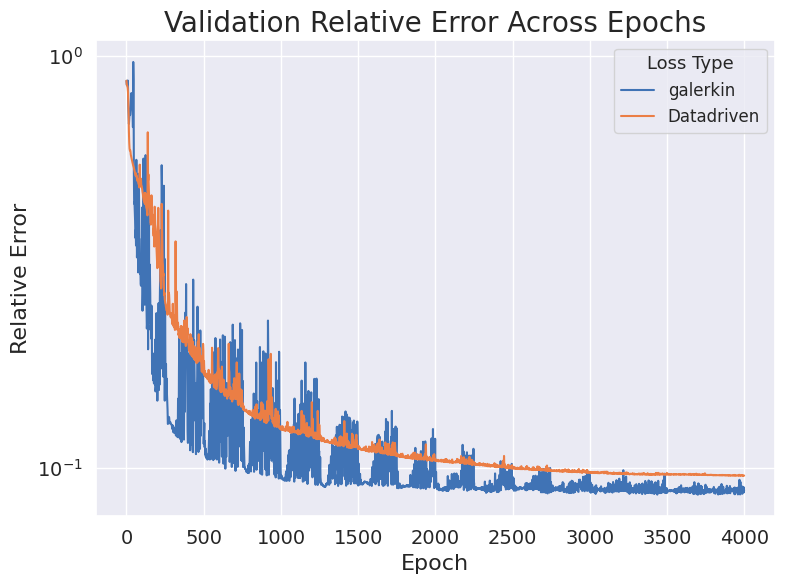
References

2024